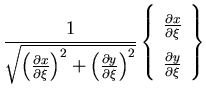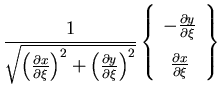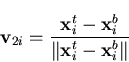Two Dimensional Element Mechanics

Next: Geometric Description Up: Degenerated Isoparametric Shell Element Previous: Reduced Selective Integration

Two Dimensional Element Mechanics

**Figure 2.4:** Coordinate Systems for Plane Shell Elements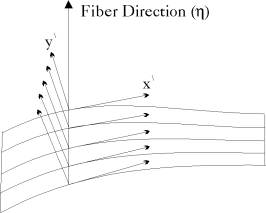

The two dimensional shell element is deduced from the three dimensional shell element presented in the previous section. The formulation is reduced by omitting one coordinate out of each of the coordinate systems used, Figure (2.4), and replacing the three dimensional plasticity problem with a plane one. The lamina coordinate system and its transformation matrix 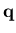${\bf q}$ are given in this case as

$\displaystyle {\bf x'}$	=	$\displaystyle \frac{1}{\sqrt{\left( \frac{\partial x}{\partial \xi} \right)^2+ ... ...partial x}{\partial \xi}\\ \frac{\partial y}{\partial \xi} \end{array}\right\}$	(47)
$\displaystyle {\bf y'}$	=	$\displaystyle \frac{1}{\sqrt{\left( \frac{\partial x}{\partial \xi} \right)^2+ ... ...partial y}{\partial \xi}\\ \frac{\partial x}{\partial \xi} \end{array}\right\}$	(48)
$\displaystyle {\bf q}$	=	$\displaystyle \left[ {\bf x'} \; {\bf y'} \right]^T$	(49)

The fiber direction v_2i at node i is given by

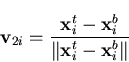$\begin{displaymath}{\bf v}_{2i}=\frac{ {\bf x}_i^t-{\bf x}_i^b }{ \Vert {\bf x}_i^t-{\bf x}_i^b \Vert} \end{displaymath}$

(50)

A. Zeiny
2000-09-06