



Next: Mass Matrix Up: Two Dimensional Element Mechanics Previous: Kinematic Description
As mentioned in the previous section, the following definition of the strain vector is required to support the selective reduced integration
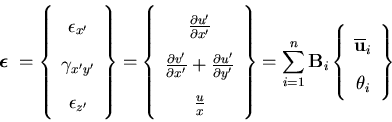 | (60) |
in which 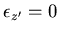 in case of plane shell. This definition yields the following strain-displacement matrix
in case of plane shell. This definition yields the following strain-displacement matrix
![\begin{displaymath}{\bf B}_i = \left[ \begin{array}{cc}
{\bf B}^u_{MN} & B^\th...
...ta_{TS} \\
{\bf B}^u_H & B^\theta_H
\end{array} \right] \\
\end{displaymath}](img184.gif) | (61) |
where the subscript H denotes the hoop strain components which are non-zero only in case of axisymmetric shell. In order to find the strain displacement matrix, the displacement vector given by Equation (2.58) is transformed to the lamina coordinate system. Thus,
![\begin{displaymath}{\bf u'}=\sum_{i=1}^{n} N_i (\xi) \left[ {\bf q} \overline{{\bf u}}_i
+ \frac{t_i \eta }{2} {\bf q R_i} \theta_i \right]
\end{displaymath}](img185.gif) | (62) |
Taking the derivative of 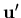 with respect to x' and y' gives
with respect to x' and y' gives
Thus, the components of the strain-displacement matrix are given as
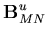 | = | ![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial N_i}{\partial x'} & 0
\end{array}\right]
{\bf q}$](img188.gif) | (65) |
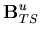 | = | ![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial N_i}{\partial y'} & \frac{\partial N_i}{\partial x'}
\end{array}\right]
{\bf q}$](img189.gif) | (66) |
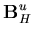 | = | ![$\displaystyle \left[ \begin{array}{cc}
\frac{N_i}{x} & 0
\end{array}\right]$](img191.gif) | (67) |
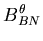 | = | ![$\displaystyle \frac{t_i }{2}
\left[ \begin{array}{cc}
\frac{ \partial \left(\eta N_i \right) }{\partial x'} & 0
\end{array}\right]
{\bf q}{\bf R}_i$](img193.gif) | (68) |
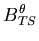 | = | ![$\displaystyle \frac{t_i }{2}
\left[ \begin{array}{cc}
\frac{\partial \left(\eta...
...rtial \left(\eta N_i \right) }{\partial x'}
\end{array}\right]
{\bf q}{\bf R}_i$](img195.gif) | (69) |
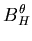 | = | ![$\displaystyle \left[ \begin{array}{cc}
\frac{\eta t_i N_i }{2x } & 0
\end{array}\right] \left\{ R_i\right\}$](img197.gif) | (70) |




Next: Mass Matrix Up: Two Dimensional Element Mechanics Previous: Kinematic Description A. Zeiny
2000-09-06 

![\begin{displaymath}{\bf B}_i = \left[ \begin{array}{cc}
{\bf B}^u_{MN} & B^\th...
...ta_{TS} \\
{\bf B}^u_H & B^\theta_H
\end{array} \right] \\
\end{displaymath}](img184.gif)
![\begin{displaymath}{\bf u'}=\sum_{i=1}^{n} N_i (\xi) \left[ {\bf q} \overline{{\bf u}}_i
+ \frac{t_i \eta }{2} {\bf q R_i} \theta_i \right]
\end{displaymath}](img185.gif)
![$\displaystyle \sum_{i=1}^{n} \left[ \frac{\partial N_i }{\partial x'}
{\bf q} \...
...rac{\partial\left( \eta N_i \right) }{\partial x'}
{\bf q R_i} \theta_i \right]$](img186.gif)
![$\displaystyle \sum_{i=1}^{n}\left[ \frac{\partial N_i }{\partial y'}
{\bf q} \o...
...rac{\partial\left( \eta N_i \right) }{\partial y'}
{\bf q R_i} \theta_i \right]$](img187.gif)
![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial N_i}{\partial x'} & 0
\end{array}\right]
{\bf q}$](img188.gif)
![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial N_i}{\partial y'} & \frac{\partial N_i}{\partial x'}
\end{array}\right]
{\bf q}$](img189.gif)
![$\displaystyle \left[ \begin{array}{cc}
\frac{N_i}{x} & 0
\end{array}\right]$](img191.gif)
![$\displaystyle \frac{t_i }{2}
\left[ \begin{array}{cc}
\frac{ \partial \left(\eta N_i \right) }{\partial x'} & 0
\end{array}\right]
{\bf q}{\bf R}_i$](img193.gif)
![$\displaystyle \frac{t_i }{2}
\left[ \begin{array}{cc}
\frac{\partial \left(\eta...
...rtial \left(\eta N_i \right) }{\partial x'}
\end{array}\right]
{\bf q}{\bf R}_i$](img195.gif)
![$\displaystyle \left[ \begin{array}{cc}
\frac{\eta t_i N_i }{2x } & 0
\end{array}\right] \left\{ R_i\right\}$](img197.gif)