



Next: Two Dimensional Element Mechanics Up: Three Dimensional Element Mechanics Previous: Fiber Numerical Integration
It is well known that certain class of problems produce excessively stiff solutions when the degenerated shell elements are used to solve them. This is attributed to that the degenerated shell elements are not capable to represent pure bending without shear or membrane effects which causes the shear locking and membrane locking phenomena. The shear locking phenomenon is caused by two main reasons
- 1.
- Some shape functions lead automatically to shear in pure bending because the transverse shear energy does not diminish as desired if the shell becomes thin
- 2.
- Sometimes, the transverse shear stiffness dominates the bending stiffness leading to an ill conditioned stiffness matrix.
Membrane locking is present in most curved elements but is less pronounced for higher order interpolation polynomials. It should be pointed out that facet shell elements which are initially free from membrane locking become curved in large displacement analyses and therefore may show considerable locking during bending deformation. Several schemes have been proposed in order to avoid locking. The most popular procedures are uniform or selectively reduced integration. This may result in undesired internal mechanism which produces hour-glass modes. Even if these zero energy modes do not exist at the beginning, they may show up in a later deformed stage. Some procedures are available to control these hour-glass modes.
The method used in this work is the so called b-treatment. In this method, the reduced components of the 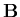 matrix are replaced by an equivalent component
matrix are replaced by an equivalent component 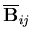 which is computed from
which is computed from
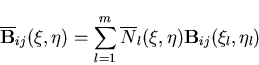 | (45) |
where 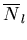 are the shape functions obtained by considering nodes at the quadrature points, and
are the shape functions obtained by considering nodes at the quadrature points, and 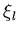 and
and 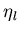 are the natural coordinates of the reduced integration points. The strain-displacement matrix is then rewritten as
are the natural coordinates of the reduced integration points. The strain-displacement matrix is then rewritten as
![\begin{displaymath}B = \left[ \begin{array}{cc}
\overline{B}^u_{MN} & B^\theta...
... \overline{\overline{B}}^\theta_{TS}
\end{array} \right] \\
\end{displaymath}](img164.gif) | (46) |
where different number of bars represents components that are integrated using different reduced integration rules.




Next: Two Dimensional Element Mechanics Up: Three Dimensional Element Mechanics Previous: Fiber Numerical Integration A. Zeiny
2000-09-06 ![]() matrix are replaced by an equivalent component
matrix are replaced by an equivalent component ![]() which is computed from
which is computed from 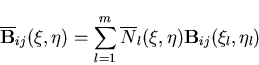
![\begin{displaymath}B = \left[ \begin{array}{cc}
\overline{B}^u_{MN} & B^\theta...
... \overline{\overline{B}}^\theta_{TS}
\end{array} \right] \\
\end{displaymath}](img164.gif)