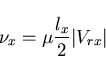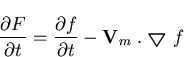Next: Discrete Finite Element Implementation Up: Finite Element Discretization Previous: Isoparametric Liquid Element Formulation
liquid sloshing is defined to be the free surface gravity waves caused by an excitation to a liquid domain. Figure (4.3) shows the geometry of the problem of liquid sloshing in a rigid tank. In the special case of rigid tank, the translational motion of the liquid boundaries are directly proportional to the ground excitation.
Figure 4.3: Geometry of the Nonlinear Liquid Sloshing in a Rigid Tank |
The normal velocity of the boundaries is then given by
where 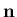 is the normal to the liquid boundary, (rx,ry,rz) is the position vector of a generic point on the liquid boundary,
is the normal to the liquid boundary, (rx,ry,rz) is the position vector of a generic point on the liquid boundary, 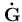 is the ground translation velocity vector and
is the ground translation velocity vector and 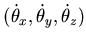 is the ground rotational velocity vector. In plane problems, Equation (4.27) is reduced to
is the ground rotational velocity vector. In plane problems, Equation (4.27) is reduced to
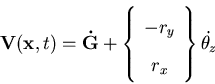 | (154) |
The strong form of the boundary value problem that represent the nonlinear liquid sloshing in a rigid tank is stated as follows:
Given ![$v_n({ \bf x},t):\Gamma_w\times [0,T]\rightarrow {\bf R}$](img406.gif) , the initial free surface
, the initial free surface 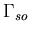 , and the initial conditions of the potential function
, and the initial conditions of the potential function 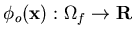 , find
, find ![$\phi({ \bf x},t): \overline{\Omega}_f \times [0,T] \rightarrow {\bf R}$](img409.gif) and
and ![$\Gamma_s\times [0,T]\rightarrow {\bf R}$](img410.gif) such that
such that
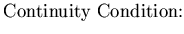 | 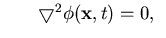 | 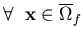 | (155) |
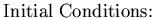 | 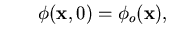 | 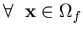 | (156) |
| | 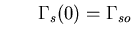 | | (157) |
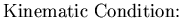 | 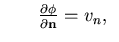 | 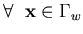 | (158) |
 | 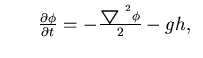 | 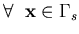 | (159) |
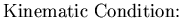 | 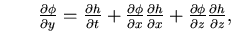 | 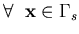 | (160) |
where 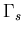 is the free surface boundary,
is the free surface boundary, 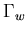 is liquid boundary in contact with the tank wall or base plate and h is the free surface elevation. Equation (4.34) represents the dynamic condition that comes from prescribing the pressure value at the free surface in Bernulli's equation, while Equation (4.35) represents the kinematic condition that enforces the vertical velocity compatibility between the free surface and the liquid domain.
is liquid boundary in contact with the tank wall or base plate and h is the free surface elevation. Equation (4.34) represents the dynamic condition that comes from prescribing the pressure value at the free surface in Bernulli's equation, while Equation (4.35) represents the kinematic condition that enforces the vertical velocity compatibility between the free surface and the liquid domain. As a result of the simplified assumptions, lack of viscosity sometimes causes undesirable contribution from the high frequency components in the numerical solution of the problem. This contribution is undesirable because of the high frequency modes in the solution that are poorly represented in the discritized system. Any wave that has a length shorter than the element width is not represented adequately due to the limited order of the shape functions. As a result, dispersion error may develop in the solution of some problems. This occurs, sometimes, when the liquid is in the resonance zone or when the excitation level is relatively high. Numerical dissipation may be used then to damp out the high frequency wave components propagating near the free surface. A numerical dissipation term was suggested by Chen [32] for the two-dimensional solution of the problem. He reported that this term has a little effect on the low frequency modes that govern the solution. After incorporating the numerical dissipation, Equation (4.35) may be rewritten in the two-dimensional case as
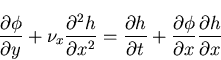 | (161) |
where 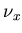 is the damping parameters given as function of the mesh density, lx, and the wave convection speed relative to the mesh
is the damping parameters given as function of the mesh density, lx, and the wave convection speed relative to the mesh 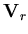 as
as
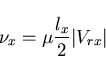 | (162) |
where lx is taken as the width of the liquid element below the free surface in the x direction and 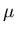 is a parameter varies between 0 and 1 to tune the damping globally. In addition, the simplified assumptions, sometimes, causes physical instability of the numerical solution used when the free surface slope is very steep,
is a parameter varies between 0 and 1 to tune the damping globally. In addition, the simplified assumptions, sometimes, causes physical instability of the numerical solution used when the free surface slope is very steep, 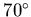 to
to 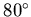 . This is attributed to the wave breaking phenomenon which is not incorporated into the current model. This is very likely to occur when the liquid is in the resonance zone, e.g. Figure (4.23), or when the excitation level is relatively high, e.g. Figure (4.24).
. This is attributed to the wave breaking phenomenon which is not incorporated into the current model. This is very likely to occur when the liquid is in the resonance zone, e.g. Figure (4.23), or when the excitation level is relatively high, e.g. Figure (4.24). In case of large amplitude surface waves, it is desirable to update the mesh to follow the liquid boundaries and to avoid distorted elements. In such a case, the time derivatives of any spatial function should be modified to account for mesh speed according to the following relation
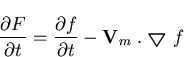 | (163) |
where 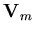 is the mesh speed and F is the function defined with respect to the fixed coordinate system while f is the function defined with respect to the moving mesh.
is the mesh speed and F is the function defined with respect to the fixed coordinate system while f is the function defined with respect to the moving mesh.




Next: Discrete Finite Element Implementation Up: Finite Element Discretization Previous: Isoparametric Liquid Element Formulation A. Zeiny
2000-09-06 
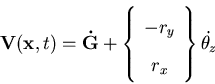
![]() , the initial free surface
, the initial free surface ![]() , and the initial conditions of the potential function
, and the initial conditions of the potential function ![]() , find
, find ![]() and
and ![]() such that
such that