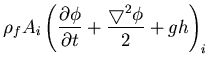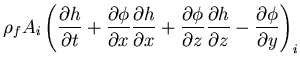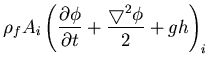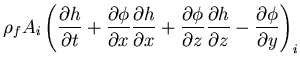next up previous contents
Next: Continuous Finite Element Implementation Up: Nonlinear Liquid Sloshing in Previous: Nonlinear Liquid Sloshing in

Discrete Finite Element Implementation

Discrete finite element implementation is achieved by enhancing the isoparametric element developed in Section 4.2.1 to model large amplitude free surface liquid sloshing in rigid tank. This is performed by enforcing the nonlinear dynamic and kinematic conditions given by Equations (4.34) and (4.35) directly on each of the free surface nodes iteratively, as follows

$\displaystyle \left(R_d \right)_i$=$\displaystyle \rho_f A_i \left(\frac{\partial \phi}{\partial t} +\frac{\bigtriangledown^2 \phi}{2} + gh\right)_i$(164)
$\displaystyle \left(R_k\right)_i$=$\displaystyle \rho_f A_i \left(\frac{\partial h}{\partial t} +\frac{\partial \p... ...tial z} \frac{\partial h}{\partial z}-\frac{\partial \phi}{\partial y}\right)_i$(165)

where Ai is the liquid free surface node tributary area projected in the horizontal plane, h is the free surface elevation, and (Rd)i and (Rk)i are the residuals corresponding to the dynamic and the kinematic equations at the node after iteration i, respectively. Physically, Rd represent the pressure force applied at the free surface node due to violation of the dynamic condition, while Rk is the discharge vector at the free surface node resulting from violating the kinematic condition. At equilibrium, the global residual vector of the entire system should be zero, which means that both the dynamic and kinematic conditions are satisfied at the free surface nodes. Taking the first variation of Rk and Rd gives, after linearization, the following modified Newton-Rapson Iterative scheme at each free surface node

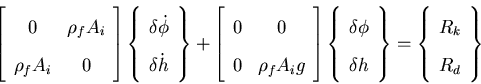 \begin{displaymath}\left[ \begin{array}{ccc} 0 & \rho_f A_i \\ \rho_f A_i & ... ...\left\{ \begin{array}{c} R_k \\ R_d \end{array} \right\} \end{displaymath}(166)

It should be pointed out that the variation of the liquid velocity and free surface slopes are ignored in Equation (4.41). This linearized version of the iterative scheme yields a symmetric coefficient matrix on the left hand side, however, it requires few more iterations to satisfy equilibrium. Although nonlinear schemes may be faster to converge, but they produce a nonsymmetric coefficient matrix on the left hand side, which requires almost double of the symmetric storage and computational cost.

next up previous contents
Next: Continuous Finite Element Implementation Up: Nonlinear Liquid Sloshing in Previous: Nonlinear Liquid Sloshing in
A. Zeiny
2000-09-06