



Next: Nonlinear Liquid Sloshing in Up: Finite Element Discretization Previous: Finite Element Discretization
Isoparametric Liquid Element Formulation
The strong form of the steady state velocity potential flow of incompressible liquid may be stated as follows:
Given 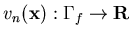 find
find 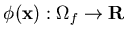 such that
such that
where vn is the prescribed normal velocity across the liquid boundaries. This strong form yields the following variational equation
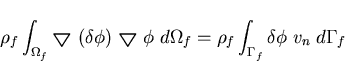 | (142) |
Following the classical isoparametric finite element discretization, the following relations are obtained;
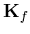 | = | 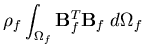 | (143) |
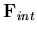 | = | 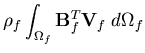 | (144) |
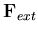 | = | 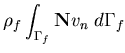 | (145) |
| | = | 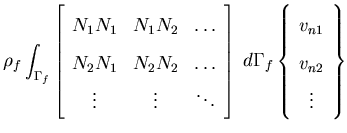 | (146) |
| | = | 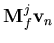 | (147) |
![$\displaystyle \left[B_f\right]$](img389.gif) | = | ![$\displaystyle \left[\begin{array}{ccc}
\frac{\partial N_1}{\partial x} & \frac{...
...rtial N_2}{\partial y} & \ldots \\
\vdots & \vdots & \ddots
\end{array}\right]$](img390.gif) | (148) |
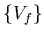 | = | 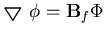 | (149) |
where 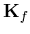 is the liquid stiffness matrix,
is the liquid stiffness matrix, 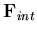 and
and 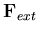 are the liquid internal and external flow vectors, respectively,
are the liquid internal and external flow vectors, respectively, 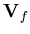 is the liquid velocity vector,
is the liquid velocity vector, 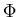 is the nodal velocity potential vector, j is the liquid element edge number that is subjected to a normal discharge of speed vn,
is the nodal velocity potential vector, j is the liquid element edge number that is subjected to a normal discharge of speed vn, 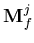 is the liquid element mass matrix for edge number jand Ni is the ith isoparametric shape function. Physically,
is the liquid element mass matrix for edge number jand Ni is the ith isoparametric shape function. Physically, 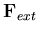 is the nodal discharge vector entering or leaving the element domain as a result of the normal velocity of the liquid across the liquid domain boundaries. This natural boundary condition ensures the normal velocity compatibility at the liquid boundaries (kinematic condition). The tangential velocity does not contribute to the discharge vector and consequently will have no effect on the continuity equation.
is the nodal discharge vector entering or leaving the element domain as a result of the normal velocity of the liquid across the liquid domain boundaries. This natural boundary condition ensures the normal velocity compatibility at the liquid boundaries (kinematic condition). The tangential velocity does not contribute to the discharge vector and consequently will have no effect on the continuity equation. 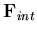 is the internal discharge vector resulting from the current gradient of the velocity potential function,
is the internal discharge vector resulting from the current gradient of the velocity potential function, 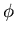 . The continuity equation is satisfied when
. The continuity equation is satisfied when 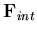 and
and 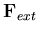 are in equilibrium. The residual discharge is then given by
are in equilibrium. The residual discharge is then given by
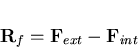 | (150) |
This residual is mainly caused by the free surface motion and the consequent remeshing of the liquid domain. This yields to an iterative modified Newton-Rapson scheme in the form
![\begin{displaymath}[K_f]\{ \delta \phi \}_i= \{R_f \}_i
\end{displaymath}](img396.gif) | (151) |
The vector 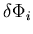 is then used to correct the velocity potential vector after the ith iteration.
is then used to correct the velocity potential vector after the ith iteration.




Next: Nonlinear Liquid Sloshing in Up: Finite Element Discretization Previous: Finite Element Discretization A. Zeiny
2000-09-06 ![]() find
find ![]() such that
such that 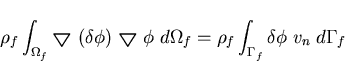
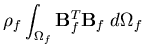
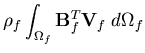
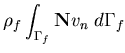
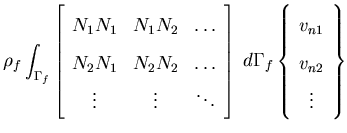
![$\displaystyle \left[\begin{array}{ccc}
\frac{\partial N_1}{\partial x} & \frac{...
...rtial N_2}{\partial y} & \ldots \\
\vdots & \vdots & \ddots
\end{array}\right]$](img390.gif)