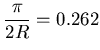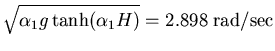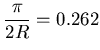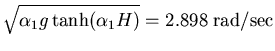next up previous contents
Next: Example 7: Free Surface Up: Two-Dimensional Examples Previous: Example 5: Nonlinear Response

Example 6: Free Surface Wave Breaking Due to Resonance

A rectangular tank of 12 ft. width and 12 ft. liquid height is subjected to the North West component of the Mexico City earthquake. The earthquake, shown in Fig (4.22) in the period domain, is found to posses strong components of period range between 1.9 and 3.0 seconds with its maximum at period 2.05 second. Using the linear analytical solution presented in [32], the liquid fundamental period is computed as follows

$\displaystyle \alpha_1$=$\displaystyle \frac{\pi}{2R}=0.262$ 
$\displaystyle \omega_1$=$\displaystyle \sqrt{\alpha_1 g \tanh(\alpha_1 H)}=2.898\;\mbox{rad/sec}$ 
T1=$\displaystyle 2.168\;\mbox{sec.}$ 

Since the free surface sloshing fundamental period is within the range of the strong components of the ground excitation, the free surface wave is expected to break. As expected, it is observed that the free surface wave breaks at time 61.8 seconds, as shown in Fig (4.23).
  
Figure 4.22: Example 6, Period Content of the Mexico City Earthquake, NW-Component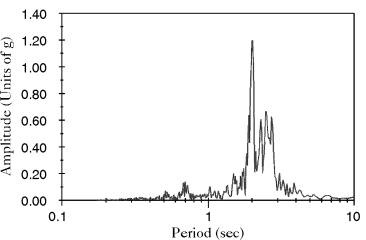


  
Figure 4.23: Example 6, Liquid Domain Just Before the Free Surface Wave Breaks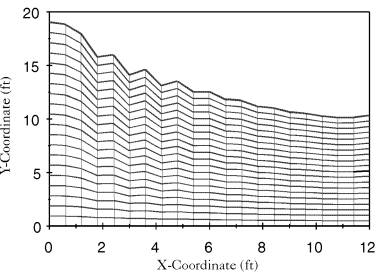

next up previous contents
Next: Example 7: Free Surface Up: Two-Dimensional Examples Previous: Example 5: Nonlinear Response
A. Zeiny
2000-09-06