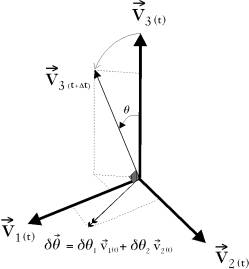
In the analysis of shells, two types of geometric nonlinearities, namely large deformation and large rotation nonlinearities, may arise. Large deformation nonlinearity is attributed to the membrane stress developed due to the midplane stretching when the shell experience large displacements as compared to its dimensions. Large rotation nonlinearity is caused by large change of element slope during the analysis. This change causes the transformation matrix to change during the analysis. It also causes the relationship between the displacement field and the nodal rotation to be trigonometric, Figure (2.5).
The objective of the analysis is to evaluate the equilibrium positions of the shell, at the discrete time points or load levels 
, 
, 
, 
, ..., t, 
. It is assumed that the solution for the kinematic and static variables for all time steps from time zero (initial configuration) to time t, inclusive, have been obtained, and that the solution for time is required next. Two approaches may be used to handle geometric nonlinearities: Updated Lagrangian description and Total Lagrangian description. The Updated Lagrangian description uses the last known deformed shell geometry at time t as a reference configuration for all variables, whereas the total Lagrangian description uses as a reference configuration the initial undeformed shell geometry. The first approach is general and suitable for both nonlinearities while the second approach in this section is developed only to handle large deformation effects.
