



Next: Computer Implementation and Testing Up: Geometric Nonlinearity Previous: Total Lagrangian Description for
In case of plane and axisymmetric shells, the formulation is deduced from the three-dimensional shell formulation. The strain vector is given by
where 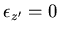 in case of plane shell. The nonlinear strain component is rewritten as
in case of plane shell. The nonlinear strain component is rewritten as
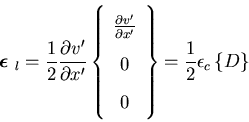 | (93) |
The coupling strain is related to the nodal degrees of freedom by
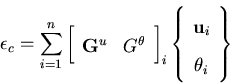 | (94) |
The matrix 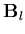 is then given by
is then given by
The stiffness matrix is then given by
![\begin{displaymath}\left[ K \right] =\int_{\Omega} \left [ \left[ B_o+B_l \right...
...igma_{x'} \left[ G \right]^T \left[ G \right]
\right] d\Omega
\end{displaymath}](img240.gif) | (98) |




Next: Computer Implementation and Testing Up: Geometric Nonlinearity Previous: Total Lagrangian Description for A. Zeiny
2000-09-06 ![$\displaystyle \left\{\begin{array}{c}
\epsilon_{x'}\\
\gamma_{x'y'}\\
\epsilo...
...}\left[\frac{\partial v'}{\partial x'}\right] ^2\\
0\\
0
\end{array} \right\}$](img232.gif)
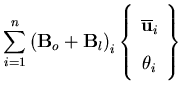
![$\displaystyle \left\{\begin{array}{c}
\epsilon_{x'}\\
\gamma_{x'y'}\\
\epsilo...
...}\left[\frac{\partial v'}{\partial x'}\right] ^2\\
0\\
0
\end{array} \right\}$](img232.gif)
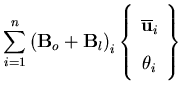
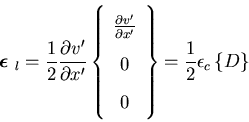
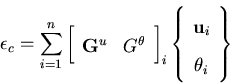
![$\displaystyle \left\{D\right\}_i
\left[\begin{array}{cc}
{\bf G}^u& G^\theta
\end{array} \right]_i$](img236.gif)
![$\displaystyle \left[ \begin{array}{cc}
0 & \frac{\partial N_i}{\partial x'}
\end{array}\right]
\left [ q \right]$](img237.gif)
![$\displaystyle \frac{t_i}{2}
\left[ \begin{array}{cc}
0 & \frac{ \partial \left(...
...i \right) }{\partial x'}
\end{array}\right]
\left [ q \right]\left\{R_i\right\}$](img239.gif)
![\begin{displaymath}\left[ K \right] =\int_{\Omega} \left [ \left[ B_o+B_l \right...
...igma_{x'} \left[ G \right]^T \left[ G \right]
\right] d\Omega
\end{displaymath}](img240.gif)