



Next: Total Lagrangian Description for Up: Geometric Nonlinearity Previous: Updated Lagrangian Description
In some cases, the deformed geometry does not show large change in slope but still indicate relatively large displacements. In such cases, it is desired to include the effect of large displacements into the strain displacement matrix and use the original geometry in the analysis. This is achieved by adding the additional membrane strains caused by the large displacements. Following the work presented in [13], the strain vector is written as
where 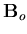 is the linear strain-displacement matrix computed as before and
is the linear strain-displacement matrix computed as before and 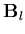 is the nonlinear strain-displacement matrix. In order to find
is the nonlinear strain-displacement matrix. In order to find 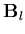 , the nonlinear strain component is rewritten as
, the nonlinear strain component is rewritten as
![\begin{displaymath}\mbox{{\boldmath$\epsilon$ }}_l = \frac{1}{2}
\left[\begin{a...
...\}
=\frac{1}{2} \left[ D \right] \left\{ \epsilon_{c} \right\}
\end{displaymath}](img220.gif) | (84) |
where 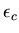 is the strain vector that couples the membrane strain to the out of plane displacements. These coupling strains are related to the nodal degrees of freedom by
is the strain vector that couples the membrane strain to the out of plane displacements. These coupling strains are related to the nodal degrees of freedom by
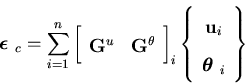 | (85) |
The matrix 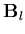 is then given by
is then given by
In large deformation analysis, the strain vector is incrementally updated after each time step by
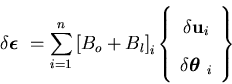 | (89) |
The stiffness matrix is then given by
![\begin{displaymath}\left[ K \right] =\int_{\Omega} \left [ \left[ B_o+B_l \right...
...a_{y'}
\end{array} \right]
\left[ G \right]
\right] d\Omega
\end{displaymath}](img231.gif) | (90) |




Next: Total Lagrangian Description for Up: Geometric Nonlinearity Previous: Updated Lagrangian Description A. Zeiny
2000-09-06 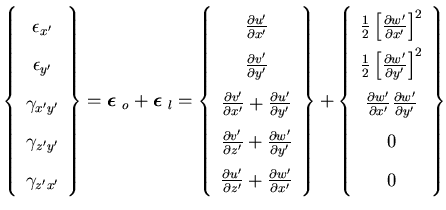
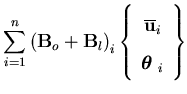
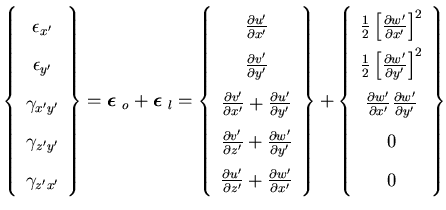
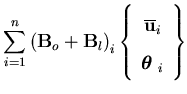
![\begin{displaymath}\mbox{{\boldmath$\epsilon$ }}_l = \frac{1}{2}
\left[\begin{a...
...\}
=\frac{1}{2} \left[ D \right] \left\{ \epsilon_{c} \right\}
\end{displaymath}](img220.gif)
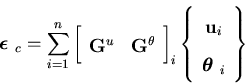
![$\displaystyle \left[D\right]_i
\left[\begin{array}{cc}
{\bf G}^u&{\bf G}^\theta
\end{array} \right]_i$](img224.gif)
![$\displaystyle \left[ \begin{array}{ccc}
0 & 0 & \frac{\partial N_i}{\partial x'...
...
0 & 0 & \frac{\partial N_i}{\partial y'}
\end{array}\right]
\left [ q \right]$](img227.gif)
![$\displaystyle \frac{t_i}{2}
\left[ \begin{array}{ccc}
0& 0 & \frac{ \partial \l...
..._i \right) }{\partial y'}
\end{array}\right]
\left [ q \right]\left[ R_i\right]$](img229.gif)
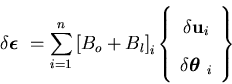
![\begin{displaymath}\left[ K \right] =\int_{\Omega} \left [ \left[ B_o+B_l \right...
...a_{y'}
\end{array} \right]
\left[ G \right]
\right] d\Omega
\end{displaymath}](img231.gif)