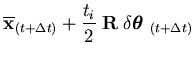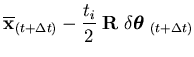next up previous contents
Next: Total Lagrangian Description for Up: Geometric Nonlinearity Previous: Geometric Nonlinearity

Updated Lagrangian Description

Geometric update is incrementally performed by superimposing the current time step incremental displacement vector to the previous time step geometry. The new geometry is then given as

  
$\displaystyle \overline{{\bf x}}_{(t+\Delta t)}$=$\displaystyle \overline{{\bf x}}_{(t)} + \delta \overline{{\bf u}}_{(t+\Delta t)}$(76)
$\displaystyle {\bf x}^t_{(t+\Delta t)}$=$\displaystyle \overline{{\bf x}}_{(t+\Delta t)} + \frac{t_i}{2}\; {\bf R} \; \delta \mbox{\boldmath$\theta$ }_{(t+\Delta t)}$(77)
$\displaystyle {\bf x}^b_{(t+\Delta t)}$=$\displaystyle \overline{{\bf x}}_{(t+\Delta t)} - \frac{t_i}{2} \; {\bf R} \; \delta \mbox{\boldmath$\theta$ }_{(t+\Delta t)}$(78)

It should be pointed out that Equations (2.77) and (2.78) are first order accurate in enforcing the fiber inextensibility condition. This condition requires that the thickness of the shell measured in the fiber direction to remain the same at all times. If the change in rotations is relatively large during the time step, an error may occur as shown in Figure (2.6). This error may be reduced either by using second order coordinate update or by using smaller time step. Alternatively, as shown in Figure (2.5), the new fiber direction and updated nodal coordinates at time $t+\Delta t$ may be obtained as
   
$\displaystyle {\bf v}_{3\;\;(t+\Delta t)}$=$\displaystyle \frac{\delta \theta_2}{\delta \theta} \sin{\delta \theta}\; {\bf ... ...n{\delta \theta}\; {\bf v}_{2\;\;(t)}+ \cos{\delta \theta}\; {\bf v}_{3\;\;(t)}$(79)
$\displaystyle {\bf x}^t_{(t+\Delta t)}$=$\displaystyle \overline{{\bf x}}_{(t+\Delta t)} + \frac{t_i}{2}\; {\bf v}_{3\;\;(t+\Delta t)}$(80)
$\displaystyle {\bf x}^b_{(t+\Delta t)}$=$\displaystyle \overline{{\bf x}}_{(t+\Delta t)} - \frac{t_i}{2} {\bf v}_{3\;\;(t+\Delta t)}$(81)


  
Figure 2.6: Geometric Update Error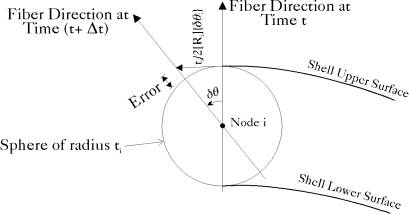

next up previous contents
Next: Total Lagrangian Description for Up: Geometric Nonlinearity Previous: Geometric Nonlinearity
A. Zeiny
2000-09-06