



Next: Kinematic Description Up: Three Dimensional Element Mechanics Previous: Coordinate Systems
The geometry of a typical three dimensional shell element is defined using the Cartesian coordinates of the top and bottom surfaces corresponding to each node, thus
or consizly as
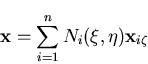 | (13) |
where the index i refer to the i'th node and n is the number of nodes per element. In order to construct the Jacobean matrix, the natural coordinate derivatives are obtained as
The Jacobean matrix required to transform derivatives between the global and natural coordinate systems is then given by
![\begin{displaymath}{\bf J } = [\frac{\partial {\bf x}}{\partial \xi} \;\; \frac{...
...\partial \eta} \;\;
\frac{\partial {\bf x}}{\partial \zeta}]^T
\end{displaymath}](img109.gif) | (17) |




Next: Kinematic Description Up: Three Dimensional Element Mechanics Previous: Coordinate Systems A. Zeiny
2000-09-06 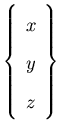
![$\displaystyle \sum_{i=1}^{n} N_i(\xi,\eta)
\left[
\frac{1+\zeta}{2}
\left\{\beg...
...{2}
\left\{\begin{array}{c}
x_i^b\\
y_i^b\\
z_i^b
\end{array}\right\}
\right]$](img100.gif)
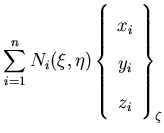

![$\displaystyle \sum_{i=1}^{n} N_i(\xi,\eta)
\left[
\frac{1+\zeta}{2}
\left\{\beg...
...{2}
\left\{\begin{array}{c}
x_i^b\\
y_i^b\\
z_i^b
\end{array}\right\}
\right]$](img100.gif)
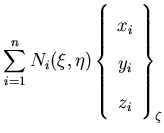
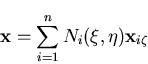
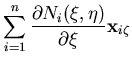
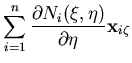
![$\displaystyle \frac{1}{2}\sum_{i=1}^{n} N_i(\xi,\eta) \left[ {\bf x}_i^t - {\bf x}_i^b \right]$](img108.gif)
![\begin{displaymath}{\bf J } = [\frac{\partial {\bf x}}{\partial \xi} \;\; \frac{...
...\partial \eta} \;\;
\frac{\partial {\bf x}}{\partial \zeta}]^T
\end{displaymath}](img109.gif)