



Next: Strain-Displacement Matrix Up: Three Dimensional Element Mechanics Previous: Geometric Description
The kinematics of the shell element are defined by invoking the isoparametric hypothesis that the same expressions are used for kinematics as for geometry with displacement variables in place of coordinate variables. This assumption leads to
![\begin{displaymath}\left\{\begin{array}{c}
u\\
v\\
w
\end{array} \right\}...
...{\zeta t_i}{2} {\bf R}_i {\mbox{\boldmath$\theta$ }}_i
\right]
\end{displaymath}](img110.gif) | (18) |
or concisely
![\begin{displaymath}{\bf u}=\sum_{i=1}^{n} N_i (\xi,\eta) \left[ \overline{{\bf u...
...{\zeta t_i}{2} {\bf R}_i {\mbox{\boldmath$\theta$ }}_i \right]
\end{displaymath}](img111.gif) | (19) |
where 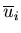 ,
, 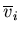 and
and 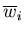 are the middle surface displacements at node i in the X, Y and Z directions, respectively, and ti is the shell thickness at node i computed as
are the middle surface displacements at node i in the X, Y and Z directions, respectively, and ti is the shell thickness at node i computed as
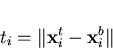 | (20) |
At this point, there are two possible choices for the rotation vector 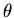 : either the rotations around the global axis or the rotations around the vectors
: either the rotations around the global axis or the rotations around the vectors 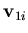 and
and 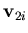 are used. Thus,
are used. Thus,
The global rotations are required when other elements that uses global rotations are used with the degenerated shell element. In such a case, special attention has to be paid to the drilling degree of freedom to avoid singular stiffness matrix.




Next: Strain-Displacement Matrix Up: Three Dimensional Element Mechanics Previous: Geometric Description A. Zeiny
2000-09-06 ![\begin{displaymath}\left\{\begin{array}{c}
u\\
v\\
w
\end{array} \right\}...
...{\zeta t_i}{2} {\bf R}_i {\mbox{\boldmath$\theta$ }}_i
\right]
\end{displaymath}](img110.gif)
![\begin{displaymath}\left\{\begin{array}{c}
u\\
v\\
w
\end{array} \right\}...
...{\zeta t_i}{2} {\bf R}_i {\mbox{\boldmath$\theta$ }}_i
\right]
\end{displaymath}](img110.gif)
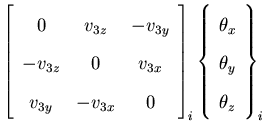
![$\displaystyle \left[\begin{array}{cc}
-{\bf v}_{2i} & {\bf v}_{1i}
\end{array}\right]
\left\{\begin{array}{c}
\theta_1 \\
\theta _2
\end{array}\right\} _i$](img119.gif)