 |
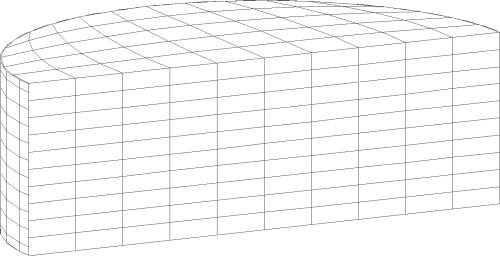
In order to evaluate the effect of flexibility of the tank wall on the response of liquid storage tanks, both the tank and the liquid were modeled using the finite element method. Figures (5.7) and (5.8) show the finite element mesh used for the broad and tall tanks, respectively. The tank base was assumed to be fixed to a rigid foundation, and consequently, the nodes of the bottom of the tank were assumed to have a specified acceleration equal to the ground acceleration. A Raleigh damping coefficient which provides 3% damping to the first mode and increasing values for the higher modes was chosen for the flexible-impulsive component. Using the added mass matrix approach presented in [103], the fundamental period of this component was found to be 0.162 sec for the broad tank and 0.189 sec for the tall tank.
Several conclusions may be drawn by observing the values in Table (5.4). For both broad and tall tanks, the acceleration at the top of the tank shell is much greater than that of the ground. Thus, the total overturning moment and base shear exerted on the flexible tank are much greater than those exerted on the rigid tank. This is due to the fact that the impulsive liquid loads arise through the acceleration of the shell. If the shell is flexible, two acceleration components must be considered: the acceleration of the undeformed shell, i.e., the ground acceleration, and the relative acceleration due to shell deformations. In a rigid tank, only the acceleration of the undeformed shell is considered leading to the noticeable difference in the magnitude of the base shear and the overturning moments.
A comparison between the response of the broad and the tall tank shows that the component of the overturning moment exerted on the tank wall in the tall tank dominates that exerted on the tank base. On the contrary, the component of the overturning moment exerted on the base of the broad tank is dominant. In addition, hoop stress near the base of the broad tank is greater than that of the tall tank. This explains the difference in the observed buckling modes of the two tanks. Previous damage observations of liquid storage tanks after major earthquakes showed that Elephant Foot buckling was the most common damage in broad tanks while tall tanks suffered Diamond-shaped buckling spreading around the circumference.
Current seismic standards for liquid storage tanks suggest the use of a response spectrum to evaluate the overturning moment exerted on the tank wall. This moment is assumed to be resisted mainly by a compression in the tank shell and a tension in the anchors. To calculate the resulting compressive stress at the bottom of the tank shell, flexural beam formula is used. This assumption yields the following compressive stress
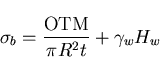 | (191) |