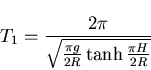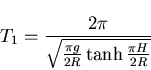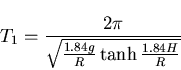Next: Anchored Tank Response Up: Nonlinear Earthquake Response of Previous: Nonlinear Earthquake Response of

Response of Tanks with Rigid Walls

Liquid motion in rigid containers reflects primarily the effect of sloshing on the response of these tanks. As a simplification for the analysis of circular cylindrical tanks, one may consider a rectangular strip in the middle of the tank and analyze it as a two-dimensional problem. Alternatively, the full three-dimensional model may be used. The linear fundamental period of the two-dimensional model is given by

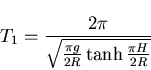$\begin{displaymath}T_1=\frac{2\pi}{ \sqrt{\frac{\pi g}{2R} \tanh \frac{\pi H}{2R}}} \end{displaymath}$

(189)

whereas for the three-dimensional model, it is given by

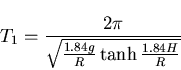$\begin{displaymath}T_1=\frac{2\pi}{ \sqrt{\frac{1.84 g}{R} \tanh \frac{1.84 H}{R}}} \end{displaymath}$

(190)

where H is the liquid depth. Although the linear fundamental periods of both the two and the three-dimensional models are close, as shown in Table (5.1), the corresponding wave heights may differ significantly. It is unconservative to use the two-dimensional model for predicting the response of cylindrical liquid storage tanks. This is attributed to the difference in the mode shapes of both models. The maximum response calculated based on two and three-dimensional models are presented and compared in Tables (5.2) and (5.3). Note that W denotes the total weight of the contained liquid and R is the tank radius. Results show that using the linear sloshing assumptions at the free surface underestimates its wave height. However, it predicts well the base shear exerted on the tank. Using the nonlinear sloshing assumptions shows that the positive sloshing amplitude is larger than the negative amplitude.

Table 5.1: Periods of Different Models for Liquid Sloshing in Rigid Tanks

	Model Type
Tank Type	2-D Model	3-D Model
Broad Tank	7.74 sec	6.89 sec
Tall Tank	4.33 sec	4.00 sec

Table 5.2: Liquid Sloshing in Rigid Containers Under El Centro Record

		Wave Height (ft)
Case		Left End	Right End	OTM/WR	Base Shear/W
Broad Tank-	2-D	2.27	2.27	0.053	0.064
Linear Sloshing	3-D	5.19	5.19	0.066	0.096
Broad Tank-	2-D	2.18	2.35	0.052	0.062
Nonlinear Sloshing	3-D	4.77	3.61	0.067	0.103
Tall Tank-	2-D	3.84	3.84	0.197	0.141
Linear Sloshing	3-D	2.23	2.23	0.216	0.155
Tall Tank-	2-D	4.24	3.56	0.196	0.143
Nonlinear Sloshing	3-D	2.32	2.36	0.216	0.155

Table 5.3: Liquid Sloshing in Rigid Containers Under the Northridge Record

		Wave Height (ft)
Case		Left End	Right End	OTM/WR	Base Shear/W
Broad Tank-	2-D	1.62	1.62	0.094	0.113
Linear Sloshing	3-D	1.52	1.52	0.086	0.125
Broad Tank-	2-D	1.59	1.64	0.092	0.105
Nonlinear Sloshing	3-D	1.47	1.59	0.089	0.127
Tall Tank-	2-D	1.64	1.64	0.379	0.262
Linear Sloshing	3-D	2.46	2.46	0.362	0.266
Tall Tank-	2-D	1.68	1.67	0.366	0.259
Nonlinear Sloshing	3-D	2.43	2.59	0.378	0.266

Figures (5.3) and (5.4) show the free surface wave heights of the two extreme opposite points on the principal diameter which parallels the earthquake excitation of the broad and tall tanks, respectively. Figures (5.5) and (5.6) present the deformed finite element mesh for both broad and tall tanks, respectively. Several ways to discretize the liquid domain were attempted to obtain the earthquake response of the liquid. It was found that the performance of an orthogonal finite element mesh yields better results and smoother free surface profile. This is attributed to the fact that the orthogonal mesh provides orthogonal mapping between the Cartesian and curvilinear coordinates, which is compatible with the stream and equipotential lines resulting from the solution of Laplace equation. Using other forms of finite element mesh in the nonlinear sloshing problem may result in a broken free surface profile and, as a result, the analysis may fail to converge.

**Figure 5.3:** Nonlinear Time History Response of the Wave Height in the Broad Tank, 3-D Model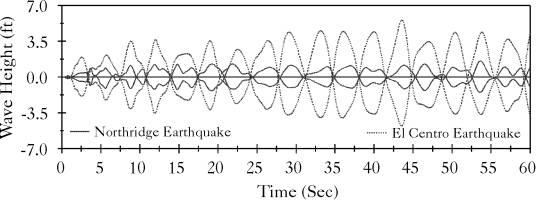

**Figure 5.4:** Nonlinear Time History Response of the Wave Height in the Tall Tank, 3-D Model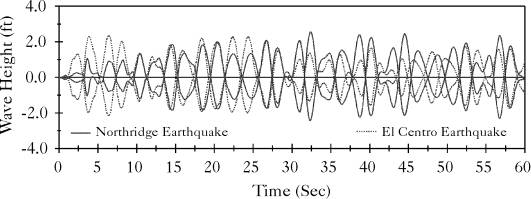

**Figure:** Deformed Liquid Domain of the Broad Tank at **t=43.5** Sec, Northridge Record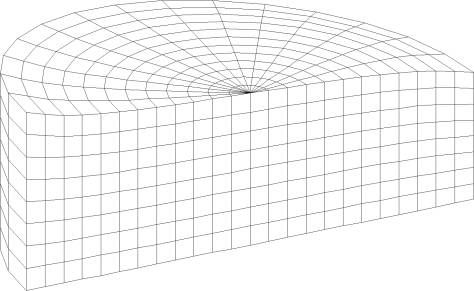

**Figure:** Deformed Liquid Domain of the Tall Tank at **t=32.5** Sec, El Centro Record

Next: Anchored Tank Response Up: Nonlinear Earthquake Response of Previous: Nonlinear Earthquake Response of

A. Zeiny
2000-09-06