Liquid Domain

Next: Coupled Liquid-Structure System Up: Variational Principles of the Previous: Structural Domain

Liquid Domain

Following the work done by Kock and Olson [141], the variational indicator of an incompressible liquid flowing under gravity field is obtained by subtracting the kinetic energy from the potential energy of an infinitesimal element of volume 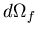$d\Omega_f$ , then integrating over the liquid domain 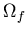$\Omega_f$ , which yields

$\begin{displaymath}\Pi_f=\int_{t_1}^{t_2} \left[ \int_{\Omega_f} \left\{ \rho_f g y - \frac{1}{2} \rho_f {\bf V.V} \right\} d\Omega_f \right] dt \end{displaymath}$

(128)

where 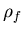$\rho_f$ is the mass density of the liquid, y is the Cartesian coordinate measured in a direction opposite to that of the gravitational acceleration g, and 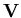${\bf V}$ is the velocity vector. The continuity condition and the kinematic condition are still need to be enforced on the liquid domain. The kinematic condition insures that the normal liquid velocity at the liquid boundary matches the rate of normal displacement of the boundary. Using Lagrange multipliers, the two conditions are added to the variational indicator as follows

$\begin{displaymath}\Pi_f=\int_{t_1}^{t_2} \left[ \int_{\Omega_f} \left\{ \rho_f... ... \lambda_2 \left\{ v_n-\dot{u}_n \right\} d\Gamma_f \right] dt \end{displaymath}$

(129)

where 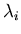$\lambda_i$ refers to the i th Lagrange Multiplier, 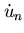$\dot{u}_n$ is the time derivative of the normal displacement of the boundary and v_n is the normal velocity at the liquid boundary. Taking variations with respect to 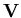${\bf V}$ gives the following Euler-Lagrange equations

$\displaystyle \delta {\bf V}:$	$\textstyle \;\;\;\; -\rho_f {\bf V} + \rho_f \mbox{{\boldmath$\bigtriangledown$ }} \lambda_1 = 0 \;\;\;\;$	$\displaystyle \mbox{ in $\Omega_f$ }$	(130)
$\displaystyle \delta v_n:$	$\textstyle \;\;\;\; \lambda_2- \rho_f \lambda_1 =0 \;\;\;\;$	$\displaystyle \mbox{ on $\Gamma_f$ }$	(131)

Thus,

$\displaystyle {\bf V}$	=	$\displaystyle \mbox{{\boldmath$\bigtriangledown$ }} \lambda_1$	(132)
$\displaystyle \lambda_2$	=	$\displaystyle \rho_f \lambda_1$	(133)

It is evident from Equation (4.7) that physically 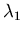$\lambda_1$ is the scalar velocity potential. Therefore, Equation (4.4) may be rewritten as

$\begin{displaymath}\Pi_f=\int_{t_1}^{t_2} \rho_f \left[ \int_{\Omega_f} \left\{... ...phi}{\partial {\bf n}}-\dot{u}_n \right\} d\Gamma_f \right] dt \end{displaymath}$

(134)

After integrating by parts, Equation (4.9) may be rewritten as

$\begin{displaymath}\Pi_f=\int_{t_1}^{t_2} \rho_f \left[ \int_{\Omega_f} \left\{... ...riangledown^2 \phi + \dot{\phi} \right\} d\Omega_f \right] dt\end{displaymath}$

(135)

or concisely,

$\begin{displaymath}\Pi_f=\int_{t_1}^{t_2} \left[ \int_{\Omega_f} P d\Omega_f \right] dt \end{displaymath}$

(136)

where P is the total pressure which may be also written as

$\begin{displaymath}P= P_o-\gamma_f\left[\frac{1}{g} \frac{\partial \phi}{\partia... ...phi. \mbox{{\boldmath$\bigtriangledown$ }} \phi}{2g}+y\right] \end{displaymath}$

(137)

where P_o is the hydrostatic pressure at the point.

Next: Coupled Liquid-Structure System Up: Variational Principles of the Previous: Structural Domain

A. Zeiny
2000-09-06