



Next: Liquid Domain Up: Variational Principles of the Previous: Variational Principles of the
Following Hamilton's principle, the energy function for the structural domain may be written as
where 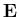 is the stress-strain matrix,
is the stress-strain matrix, 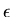 is the strain vector,
is the strain vector, 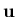 is the displacement vector,
is the displacement vector, 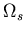 is the structural domain,
is the structural domain, 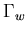 is the wet surface of the structure,
is the wet surface of the structure, 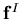 is the liquid pressure vector,
is the liquid pressure vector, 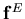 is the body force vector and
is the body force vector and 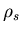 is the mass density of the structure. Setting variations on
is the mass density of the structure. Setting variations on 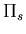 to zero gives the principle of virtual displacements
to zero gives the principle of virtual displacements
A. Zeiny
2000-09-06 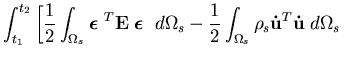
![$\displaystyle \left. \int_{\Gamma_w} {\bf u}^T {\bf f}^I \; d\Gamma_w
- \int_{\Omega_s} {\bf u}^T {\bf f}^E \;d\Omega_s
\right] dt$](img341.gif)