Condition of Sliding Contact

Next: Condition of Tension Release Up: Finite Element Formulation Previous: Condition of Sticking Contact

Condition of Sliding Contact

A contactor node c is assumed to be in sliding contact if the tangential force exceeds the frictional capacity. The sliding contact condition has to be preceded by either sticking or sliding contact condition. Thus, the penetration vector 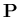${\bf P}$ on the right hand side of Equation (3.6) is set to zero. The inequality constraints to be enforced in this case are

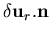$\displaystyle \delta {\bf u}_r .{\bf n}$	=	0	(115)
F_n	>	0	(116)
F_t	=	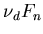$\displaystyle \nu_d F_n$	(117)

where 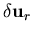$\delta {\bf u}_r$ is the incremental relative displacemnt vector, which is given by

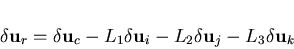$\begin{displaymath}\delta {\bf u}_r = \delta {\bf u}_c - L_1 \delta {\bf u}_i - L_2 \delta {\bf u}_j - L_3 \delta {\bf u}_k \end{displaymath}$

(118)

These constraints are enforced through the matrix 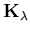${\bf K}_{\lambda}$ , and the vector ${\bf F}$ . Figure (3.5) shows a contactor node c that is in contact with the target element connected to the three nodes i, j and k. After the geometric analysis of the nodal coordinates and deformations is performed and the target element, the attached nodes and the nondimensional triangular coordinates L₁, L₂ and L₃, are determined, the vector ${\bf F}$ is computed from the residual vector resulting from the global equilibrium of node c. The normal and tangential components of the contact force are then given by

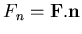$\displaystyle F_n={\bf F}.{\bf n}$			(119)
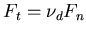$\displaystyle F_t= \nu_d F_n$			(120)

The tangential component is then applied in a direction opposite to the velocity direction at node c. The constraint matrix 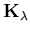${\bf K}_{\lambda}$ is given by

$\begin{displaymath}[ K_\lambda^T]= C_\lambda \left[ \begin{array}{cccccccccccc} ... ..._1&mL_1&nL_1&lL_2&mL_2&nL_2&lL_3&mL_3&nL_3 \end{array} \right] \end{displaymath}$

(121)

where l, m and n are the direction cosines of the vector normal to the target surface that contains nodes i, j and k.

**Figure 3.5:** Geometry of Sliding Contact Condition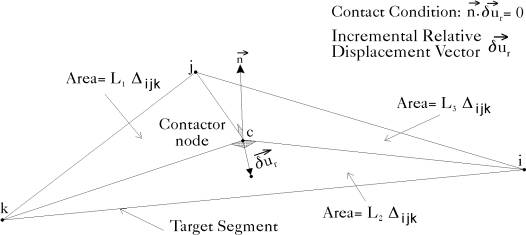

Next: Condition of Tension Release Up: Finite Element Formulation Previous: Condition of Sticking Contact

A. Zeiny
2000-09-06