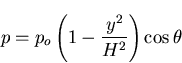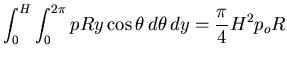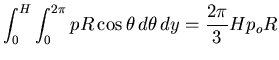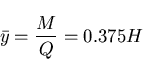Next: Conclusion Up: Nonlinear Earthquake Response of Previous: Effect of Vertical Excitation

Lateral Static Push Response of Unanchored Tanks

**Figure 5.28:** Pseudo-Dynamic Loads Applied on Tank Wall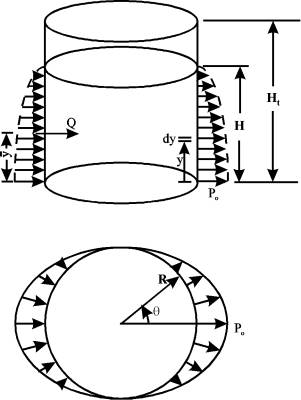

The lateral static push analysis is performed to investigate the behavior of unanchored liquid storage tanks when subjected to lateral earthquake loads. As the tank is pushed in the lateral direction, it uplifts from its foundation and develops a similar uplifting mechanism to that occurred under earthquake excitations. As shown in Figure (5.28), a hydrodynamic pressure distribution was assumed on the tank wall as

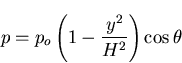$\begin{displaymath}p=p_o\left( 1-\frac{y^2}{H^2} \right) \cos \theta \end{displaymath}$

(192)

where y is the elevation of a point on the shell measured from the base, H is the fluid depth, 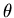$\theta$ is the angle measured from the axis of excitation and p_o is the pressure amplitude at the tank base at 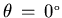$\theta\,=\,0^{\mbox{\tiny {o}}}$ . If M denotes the overturning moment about the center of the base, then

M	=	$\displaystyle \int_0^H \int_0^{2\pi} p R y\cos \theta \,d\theta\,dy = \frac{\pi}{4}H^2 p_o R$	(193)
	=	$\displaystyle 75360 \; p_o \; \; \mbox{ For broad tank}$
	=	$\displaystyle 97667 \; p_o \; \; \mbox{ For tall tank}$

and similarly, if Q is the base shear, then

Q	=	$\displaystyle \int_0^H \int_0^{2\pi} p R \cos \theta \,d\theta\,dy = \frac{2\pi}{3}H p_o R$	(194)
	=	$\displaystyle 5024 \; p_o \; \; \mbox{ For broad tank}$
	=	$\displaystyle 3617 \; p_o \; \; \mbox{ For tall tank}$

and accordingly

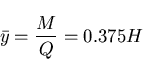$\begin{displaymath}\bar{y}= \frac{M}{Q} = 0.375 H \end{displaymath}$

(195)

Figures (5.29) and (5.30) show the finite element mesh used to model the broad and the tall tanks, respectively. The broad tank showed buckling at a value of OTM/WR=0.077 which indicates that the broad tank may have buckled during transient responses presented before. On the contrary, the tall tank did not experience buckling until it overturns. Figures (5.31) and (5.32) show that uplift displacements predicted from static analyses were larger than those predicted from dynamic analyses presented before. However, predicted axial stresses at the bottom of the tank shell were compared to those predicted from dynamic analyses.

**Figure 5.29:** Finite Element Model of the Broad Tank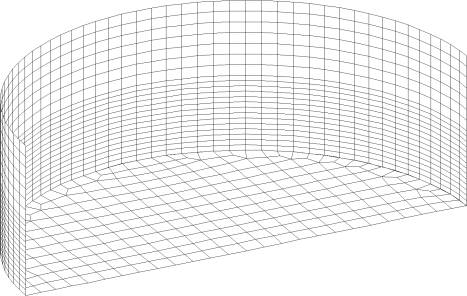

**Figure 5.30:** Finite Element Model of the Tall Tank

**Figure 5.31:** Static Response of the Broad Tank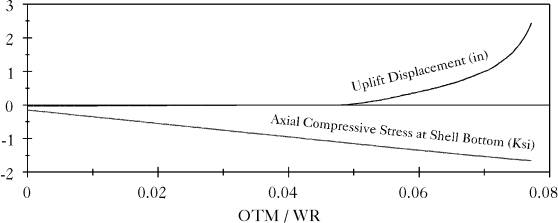

**Figure 5.32:** Static Response of the Tall Tank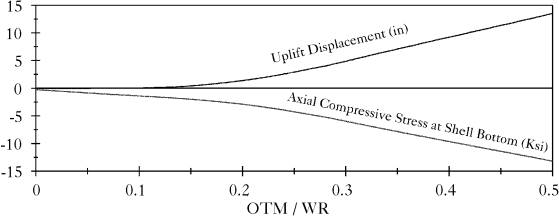

Next: Conclusion Up: Nonlinear Earthquake Response of Previous: Effect of Vertical Excitation

A. Zeiny
2000-09-06