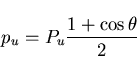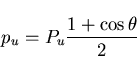Next: Longitudinal Impact of a Up: Three-Dimensional Numerical Examples Previous: Three-Dimensional Numerical Examples
A nonlinear behavior has been demonstrated by unanchored liquid storage tanks during earthquakes. Amongst the factors which contribute to such a complex behavior, there are two characteristics associated with base plate uplifting that add to the intricacy of the problem. The first complexity arises because the contact area of base plate with its supporting foundation is continually changing as uplift forces change. Secondly, the transverse deflection of the plate may become large in comparison with the base plate thickness, thereby inducing membrane forces that could not be ignored in the analysis. In this example, a thin circular plate of 1.25 cm thickness and 6 m radius was subjected to a downward hydrostatic pressure of 49.1 KN/m2 and an uplifting force acting along the periphery of the outer circle which is given by
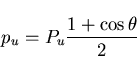 | (125) |
where Pu is the amplitude of the uplift force, and 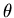 is an angle measured from the direction of the earthquake excitation. The plate has been discretized as shown in Figure (3.16). The membrane degrees of freedom along the periphery of the outer circle of the plate and the boundaries of the contact area were assumed fixed. Three cases of the rotation degrees of freedom along the periphery of the outer circle of the plate are presented in Figure (3.17): free, fully restrained and partially restrained. Results conform with those presented in [13].
is an angle measured from the direction of the earthquake excitation. The plate has been discretized as shown in Figure (3.16). The membrane degrees of freedom along the periphery of the outer circle of the plate and the boundaries of the contact area were assumed fixed. Three cases of the rotation degrees of freedom along the periphery of the outer circle of the plate are presented in Figure (3.17): free, fully restrained and partially restrained. Results conform with those presented in [13].
Figure 3.16: The Finite Element Model Used for the Plate |
Figure 3.17: Uplift Displacement vs Uplift Force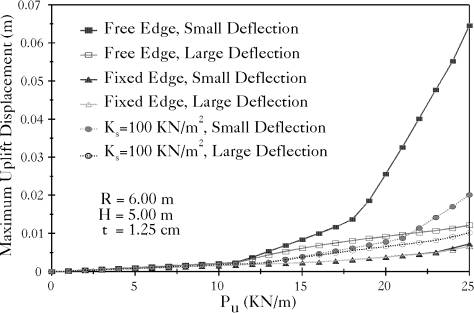 |




Next: Longitudinal Impact of a Up: Three-Dimensional Numerical Examples Previous: Three-Dimensional Numerical Examples A. Zeiny
2000-09-06