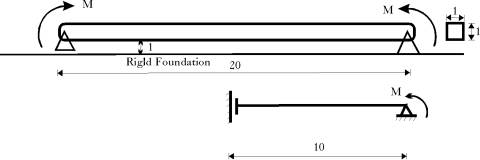
A long simply supported rectangular beam is bent by two equal end-point moments, MAs the beam deflects, it approaches, and eventually reaches, a flat rigid surface, see Figure (3.7). The material behavior of the beam is described by linear elastics model of 
and 
. Solution to this problem may be obtained by means of various linear beam theories. Also, a similar problem has been presented in [215].
The beam was uniformly discretized into 100 degenerated plane stress shell elements and symmetry was observed. A reduced selective integration technique was used to avoid shear locking phenomenon. The finite element solution qualitatively conforms with the other results, as it predicts release from the rigid surface in the middle of the beam with the increase of the applied moments. Figure (3.8) shows the deformation for different values of the applied moment M. The corresponding contact pressure between the beam and the foundation is shown in Figure (3.9). The change of beam length in contact with the foundation is shown in Figure (3.10). The support vertical reaction that represent the integration of the contact pressure over the area is show in Figure (3.11). All results are presented only for the right half of the beam.
