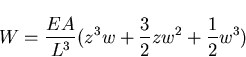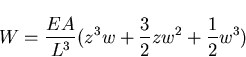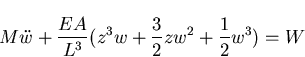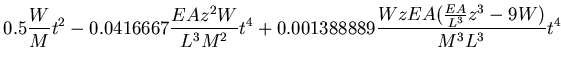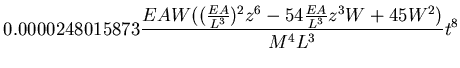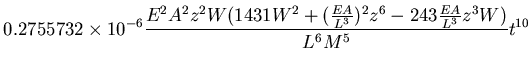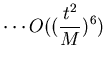Large Deflection and Rotation Analysis of a Beam Column

Next: Linear Vibration of a Up: Two-Dimensional Numerical Examples Previous: Linear and Nonlinear Buckling

Large Deflection and Rotation Analysis of a Beam Column

A beam column of length L and cross section area A is subjected to a load W, as shown in Figure (2.10). The beam is hinged from the left end, and supported from the other end by a spring of stiffness K_s and a roller. The analytical solution presented in [44] gives the following relation between the load W and the deflection w

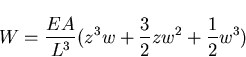$\begin{displaymath}W=\frac{EA}{L^3} (z^3 w+\frac{3}{2}z w^2+\frac{1}{2} w^3 ) \end{displaymath}$

(99)

The beam is modeled with one shell element. Different values of the spring stiffness parameter 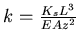$k=\frac{K_s L^3}{E A z ^ 2}$ are chosen. Figure (2.11) shows the relation between the load parameter 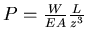$P=\frac{W}{EA}\frac{L}{z^3}$ and the deflection parameter 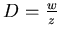$D=\frac{w}{z}$ which is found to be identical to the analytical solution. It should be pointed out that if the spring stiffness parameter is less than or equal to 0.5, then the displacement control should be used in the analysis in lou of the load control to achieve convergence.

**Figure 2.10:** Large Deflection and Rotation Analysis of a Beam Column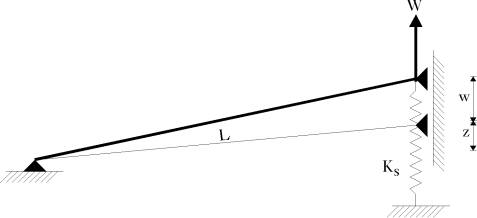

**Figure 2.11:** Large Deflection and Rotation Analysis of a Beam Column: Force-Deflection Curve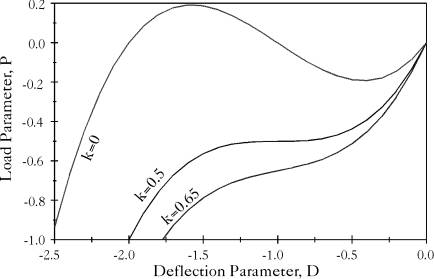

The same problem is also tested in dynamic analysis. The equation of motion is written for constant applied force W which gives

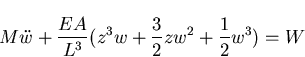$\begin{displaymath}M \ddot{w}+\frac{EA}{L^3} (z^3 w+\frac{3}{2}z w^2+\frac{1}{2} w^3 )=W \end{displaymath}$

(100)

where 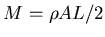$M=\rho A L / 2$ . The series solution to the equation of motion gives

w(t)	=	$\displaystyle 0.5 \frac{W}{M} t^2 -0.0416667 \frac{EA z^2W}{L^3M^2}t^4 + 0.001388889 \frac{Wz EA(\frac{EA}{L^3}z^3-9W)}{M^3L^3} t^4$
	-	$\displaystyle 0.0000248015873 \frac{EAW((\frac{EA}{L^3})^2 z^6 -54 \frac{EA}{L^3}z^3W+45W^2)}{M^4L^3} t^8$
	+	$\displaystyle 0.2755732\times10^{-6}\frac{E^2A^2z^2W (1431W^2+(\frac{EA}{L^3})^2z^6-243\frac{EA}{L^3}z^3W)} {L^6M^5}t^{10}$
	+	$\displaystyle \cdots O((\frac{t^2}{M})^6)$	(101)

The first term of the solution represent the rigid motion of the beam column with no contribution from its elasticity. This term is found to be dominant when 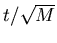$t/\sqrt{M}$ is relatively small. Figure (2.12) shows a comparison between the response time history of the analytical solution and that obtained from the program DYNAZ.

**Figure 2.12:** Large Deflection and Rotation Analysis of a Beam Column: Response Time History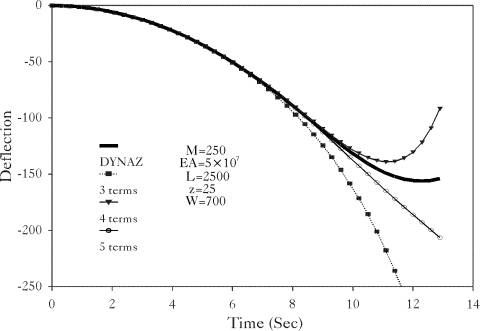

Next: Linear Vibration of a Up: Two-Dimensional Numerical Examples Previous: Linear and Nonlinear Buckling

A. Zeiny
2000-09-06