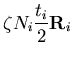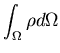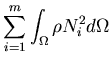Next: Fiber Numerical Integration Up: Three Dimensional Element Mechanics Previous: Strain-Displacement Matrix
The consistant mass matrix for curved shells is computed by performing a volume integration over the element domain, as follows
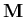 | = | 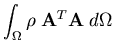 | (37) |
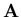 | = | ![$\displaystyle \left[ {\bf A}_1 \; {\bf A}_2 \; \cdots \right]$](img147.gif) | (38) |
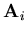 | = | ![$\displaystyle \left[ {\bf N}_i \; {\bf Z}_i \right]$](img149.gif) | (39) |
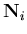 | = | ![$\displaystyle \left[ \begin{array}{ccc}
N_i&0&0\\
0&N_i&0\\
0&0&N_i
\end{array} \right]$](img151.gif) | (40) |
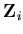 | = | 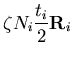 | (41) |
where the subscript i denotes the node number. For degenerated shells, the terms that correspond to the translational degrees of freedom are dominant as compared to the rotational terms. Sometimes, it is desired to diagonalize the resulting matrix to simplify the analysis and to avoid ill-conditioned mass matrix. In this work, Hinton technique is used to diagonalize the mass matrix. This is achieved by setting the entries of the lumped-mass matrix proportional to the diagonal entries of the consistant mass. The constant of proportion, selected to conserve the total element mass, is computed as follows
where Mt is the total element mass, Md is the sum of translational diagonal entries of the consistent mass matrix and m is the total number of translational degrees of freedom. The rotational diagonal and off-diagonal terms are then set to zero.




Next: Fiber Numerical Integration Up: Three Dimensional Element Mechanics Previous: Strain-Displacement Matrix A. Zeiny
2000-09-06 
![$\displaystyle \left[ \begin{array}{ccc}
N_i&0&0\\
0&N_i&0\\
0&0&N_i
\end{array} \right]$](img151.gif)
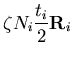
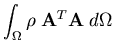
![$\displaystyle \left[ \begin{array}{ccc}
N_i&0&0\\
0&N_i&0\\
0&0&N_i
\end{array} \right]$](img151.gif)